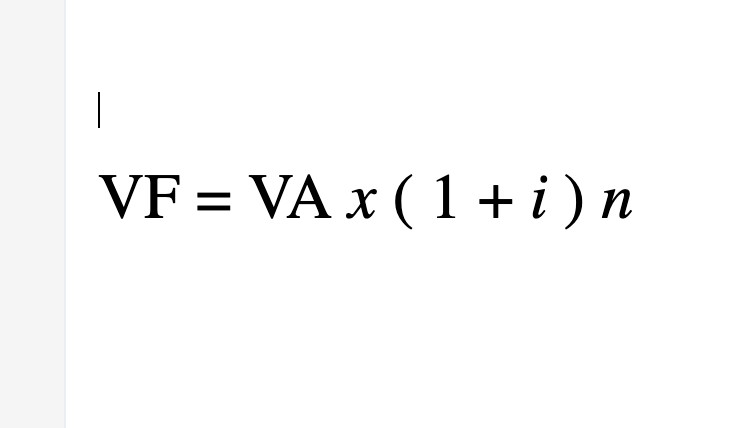Oggi vedremo la differenza tra interesse semplice ed interesse composto e come mai quest’ultimo è da tenere ben presente quando si fa un investimento, in quanto può fare la fortuna di un investitore – anche alle prime armi – se segue i dettami del value investing nell’investimento nel lungo periodo.
Cos’è l’interesse composto:
L’interesse composto è quando degli interessi si calcolano non solo sul capitale, ma anche sugli interessi fin lì generati dal capitale iniziale. Questo modo di investire si chiama anche capitalizzazione degli interessi o compounding in inglese, cioè il processo in cui i guadagni di un asset, da plusvalenze o interessi , vengono reinvestiti per generare guadagni aggiuntivi nel tempo. Questa crescita, calcolata utilizzando le funzioni esponenziali, si verifica perché l’investimento genererà guadagni sia dal suo capitale iniziale che dai guadagni accumulati dai periodi precedenti. La capitalizzazione, quindi, differisce dalla crescita lineare, in cui solo il capitale guadagna interessi ogni periodo.
Interesse composto in breve:
-
L’interesse composto è il processo in base al quale gli interessi vengono accreditati su un importo principale esistente nonché sugli interessi già pagati.
-
La composizione può quindi essere interpretata come interesse sull’interesse, il cui effetto è quello di amplificare i rendimenti dell’interesse nel tempo, il cosiddetto “miracolo della composizione”.
-
Quando le banche o gli istituti finanziari accreditano interessi composti, utilizzeranno un periodo di composizione come annuale, mensile o giornaliero.
Capire e sfruttare l’interesse composto:
L’interesse composto o capitalizzazione degli interessi, si riferisce tipicamente all’aumento del valore di un bene a causa degli interessi guadagnati sia su un interesse principale che su quello accumulato. Questo fenomeno, che è una realizzazione diretta del concetto di valore temporale del denaro (VTD), è noto anche come interesse composto.
L’interesse composto funziona sia sulle attività che sulle passività. Sebbene la capitalizzazione aumenti più rapidamente il valore di un’attività, può anche aumentare la quantità di denaro dovuta su un prestito, poiché gli interessi si accumulano sul capitale non pagato e sugli interessi precedenti.
Per illustrare come funziona la composizione, supponiamo che 10.000 euro siano detenuti in un conto che paga un interesse del 5% all’anno. Dopo il primo anno o periodo di capitalizzazione, il totale nel conto è salito a 10.500 euro, un semplice guadagno di 500 euro di interesse aggiunto al capitale di 10.000 euro . Nel secondo anno, il conto realizza una crescita del 5% sia sul capitale originario che sui 500 euro di interessi del primo anno, con un conseguente guadagno del secondo anno di 525 euro e un saldo di 11.025 euro. Dopo 10 anni, ipotizzando l’assenza di prelievi e un tasso di interesse costante del 5%, l’account crescerebbe fino a 16.288,95 euro.
LEGGI ANCHE : Buy and Hold –
Considerazioni speciali
La formula per il valore futuro (VF) di un’attività corrente si basa sul concetto di interesse composto. Prende in considerazione il valore attuale di un’attività, il tasso di interesse annuo e la frequenza di capitalizzazione (o il numero di periodi di capitalizzazione) per anno e il numero totale di anni. La formula generalizzata per l’interesse composto è:
- VF = valore futuro
- VA = valore attuale
- i = il tasso di interesse annuo
- n = il numero di periodi di capitalizzazione all’anno
- t = il numero di anni
Periodi di compounding aumentati
Gli effetti della composizione si rafforzano con l’aumentare della frequenza della composizione. Assumi un periodo di tempo di un anno. Più periodi di composizione durante questo anno, maggiore è il valore futuro dell’investimento, quindi, naturalmente, due periodi di composizione all’anno sono migliori di uno e quattro periodi di composizione all’anno sono migliori di due.
Per illustrare questo effetto, si consideri il seguente esempio con la formula precedente. Supponiamo che un investimento di $ 1 milione guadagni il 20% all’anno. Il valore futuro risultante, basato su un numero variabile di periodi di composizione, è:
- Interessi composti annuali (n = 1): VF = 1.000.000 euro x [1 + (20% / 1)] (1 x 1) = 1.200.000 euro
- Interessi composti semestrali (n = 2): VF = 1.000.000 euro x [1 + (20% / 2)] (2 x 1) = 1.210.000 euro
- Interessi composti trimestrali (n = 4): VF = 1.000.000 euro x [1 + (20% / 4)] (4 x 1) = 1.215.506 euro
- Interesse composto mensile (n = 12): VF = 1.000.000 euro x [1 + (20% / 12)] (12 x 1) = 1.219.391 euro
- Interesse composto settimanale (n = 52): VF = 1.000.000 euro x [1 + (20% / 52)] (52 x 1) = 1.220.934 euro
- Interesse composto giornaliero (n = 365): VF = 1.000.000 euro x [1 + (20% / 365)] (365 x 1) = 1.221.336 euro
Come evidente, il valore futuro aumenta di un margine inferiore anche se il numero di periodi di composizione all’anno aumenta in modo significativo. La frequenza della capitalizzazione per un determinato periodo di tempo ha un effetto limitato sulla crescita di un investimento. Questo limite, basato sul calcolo, è noto come composizione continua e può essere calcolato utilizzando la formula:
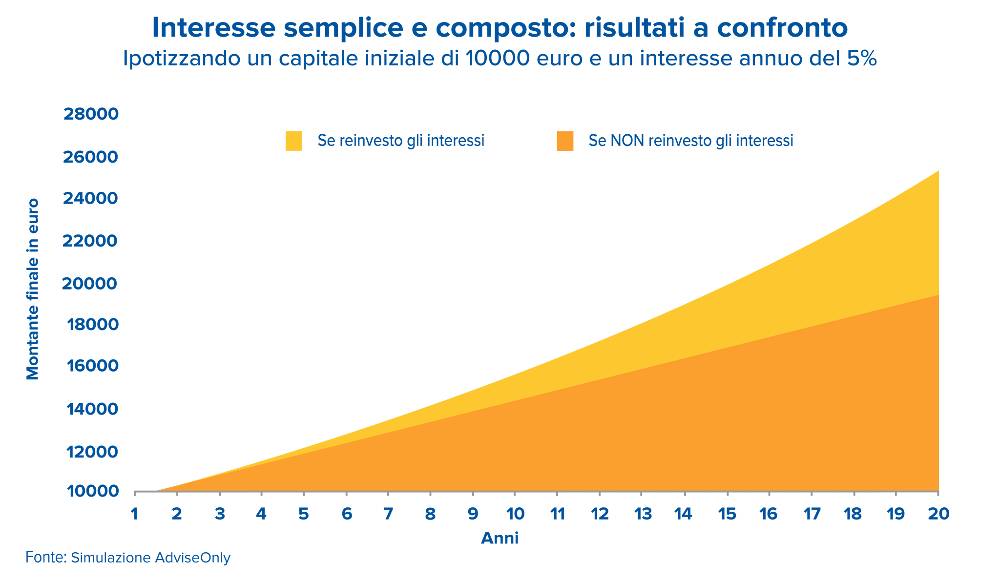
L’importanza dell’ interesse composto negli investimenti
La capitalizzazione è cruciale nella finanza e i guadagni attribuibili ai suoi effetti sono la motivazione alla base di molte strategie di investimento. Ad esempio, molte società offrono piani di reinvestimento dei dividendi che consentono agli investitori di reinvestire i propri dividendi in contanti per acquistare ulteriori azioni. Reinvestire in più di queste azioni che pagano dividendi, aumenta i rendimenti degli investitori perché l’aumento del numero di azioni aumenterà costantemente il reddito futuro dai pagamenti dei dividendi, assumendo dividendi costanti.
Investire in azioni di crescita dei dividendi, oltre a reinvestire i dividendi, aggiunge un altro livello di capitalizzazione a questa strategia che alcuni investitori chiamano “doppia capitalizzazione“. In questo caso, non solo i dividendi vengono reinvestiti per acquistare più azioni, ma queste azioni di crescita dei dividendi stanno anche aumentando i loro pagamenti per azione.
Facendo un altro esempio dell’investimento più semplice e conosciuto: se io investo 1.000 euro in azioni e quel giorno il prezzo sale dell’1%, ecco che a fine giornata avrò 1.010 euro. A quel punto il secondo giorno se il titolo guadagnerà un altro + 1% quell’1% andrà calcolato sui 1.010 euro, e non più solo sui 1.000 euro.
Se queste cifre dell’esempio possono sembrarvi piccole ed insignificanti, pensate a cosa può accadere quando si compra un pacchetto azionario che cresce del + 100 % in 1 anno come è accaduto recentemente per Amazon ( AMZN ) , per esempio.
ESEMPI DI INTERESSE COMPOSTO SU AZIONI
1. Se compro 10.000 euro in azioni e le tengo per 10 anni, considerando una crescita del 5% ogni anno, dopo 10 anni quanto sarà la somma a mia disposizione ( considerando l’interesse composto)?
Per calcolare la somma che avrai a disposizione dopo 10 anni con un tasso di crescita del 5% all’anno e l’interesse composto, puoi utilizzare la formula dell’interesse composto:
A = P(1 + r/n)^(nt)
Dove:
A = L’ammontare finale comprensivo degli interessi
P = L’importo principale iniziale
r = Tasso di interesse annuale (in decimale)
n = Numero di volte in cui l’interesse viene composto all’anno
t = Numero totale di anni
Nel tuo caso, hai 10.000 euro (P) e un tasso di crescita del 5% (r = 0.05). Supponiamo che l’interesse venga composto una volta all’anno (n = 1) per 10 anni (t = 10). Sostituendo questi valori nella formula, otteniamo:
A = 10,000(1 + 0.05/1)^(1*10)
= 10,000(1 + 0.05)^10
= 10,000(1.05)^10
≈ 16,386.93 euro
Quindi, dopo 10 anni, con una crescita del 5% all’anno e l’interesse composto, avrai circa 16,386.93 euro a tua disposizione.
2. Se compro 30.000 euro in azioni e le tengo per 10 anni, considerando una crescita del 5% ogni anno, dopo 10 anni quanti soldi avrò dopo 10 anni? ( considerando l’interesse composto)?
Per calcolare la somma che avrai a disposizione dopo 10 anni con un tasso di crescita del 5% all’anno e l’interesse composto, puoi utilizzare la formula dell’interesse composto:
A = P(1 + r/n)^(nt)
Dove:
A = L’ammontare finale comprensivo degli interessi
P = L’importo principale iniziale
r = Tasso di interesse annuale (in decimale)
n = Numero di volte in cui l’interesse viene composto all’anno
t = Numero totale di anni
Nel tuo caso, hai 30.000 euro (P) e un tasso di crescita del 5% (r = 0.05). Supponiamo che l’interesse venga composto una volta all’anno (n = 1) per 10 anni (t = 10). Sostituendo questi valori nella formula, otteniamo:
A = 30,000(1 + 0.05/1)^(1*10)
= 30,000(1 + 0.05)^10
= 30,000(1.05)^10
≈ 48,366.93 euro
Quindi, dopo 10 anni, con una crescita del 5% all’anno e l’interesse composto, avrai circa 48,366.93 euro a tua disposizione.
3. Se compro 10.000 euro in azioni e le tengo per 10 anni, considerando una crescita del 15% ogni anno, dopo 10 anni quanti soldi avrò dopo 10 anni? ( considerando l’interesse composto)?
Per calcolare la somma che avrai a disposizione dopo 10 anni con un tasso di crescita del 15% all’anno e l’interesse composto, possiamo utilizzare la formula dell’interesse composto:
A = P(1 + r/n)^(nt)
Dove:
A = L’ammontare finale comprensivo degli interessi
P = L’importo principale iniziale
r = Tasso di interesse annuale (in decimale)
n = Numero di volte in cui l’interesse viene composto all’anno
t = Numero totale di anni
Nel tuo caso, hai 10.000 euro (P) e un tasso di crescita del 15% (r = 0.15). Supponiamo che l’interesse venga composto una volta all’anno (n = 1) per 10 anni (t = 10). Sostituendo questi valori nella formula, otteniamo:
A = 10,000(1 + 0.15/1)^(1*10)
= 10,000(1 + 0.15)^10
= 10,000(1.15)^10
≈ 40,720.46 euro
Quindi, dopo 10 anni, con una crescita del 15% all’anno e l’interesse composto, avrai circa 40,720.46 euro a tua disposizione.
4. Se compro 20.000 euro in azioni e le tengo per 10 anni, considerando una crescita del 15% ogni anno, dopo 10 anni quanti soldi avrò dopo 10 anni? ( considerando l’interesse composto)?
Per calcolare la somma che avrai a disposizione dopo 10 anni con un tasso di crescita del 15% all’anno e l’interesse composto, possiamo utilizzare la formula dell’interesse composto:
A = P(1 + r/n)^(nt)
Dove:
A = L’ammontare finale comprensivo degli interessi
P = L’importo principale iniziale
r = Tasso di interesse annuale (in decimale)
n = Numero di volte in cui l’interesse viene composto all’anno
t = Numero totale di anni
Nel tuo caso, hai 20.000 euro (P) e un tasso di crescita del 15% (r = 0.15). Supponiamo che l’interesse venga composto una volta all’anno (n = 1) per 10 anni (t = 10). Sostituendo questi valori nella formula, otteniamo:
A = 20,000(1 + 0.15/1)^(1*10)
= 20,000(1 + 0.15)^10
= 20,000(1.15)^10
≈ 74,080.28 euro
Quindi, dopo 10 anni, con una crescita del 15% all’anno e l’interesse composto, avrai circa 74,080.28 euro a tua disposizione.
5. Se compro 1.000 euro in azioni e le tengo per 10 anni, considerando una crescita del 18% ogni anno, dopo 10 anni quanti soldi avrò dopo 10 anni? ( considerando l’interesse composto)?
Per calcolare la somma che avrai a disposizione dopo 10 anni con un tasso di crescita del 18% all’anno e l’interesse composto, possiamo utilizzare la formula dell’interesse composto:
A = P(1 + r/n)^(nt)
Dove:
A = L’ammontare finale comprensivo degli interessi
P = L’importo principale iniziale
r = Tasso di interesse annuale (in decimale)
n = Numero di volte in cui l’interesse viene composto all’anno
t = Numero totale di anni
Nel tuo caso, hai 1.000 euro (P) e un tasso di crescita del 18% (r = 0.18). Supponiamo che l’interesse venga composto una volta all’anno (n = 1) per 10 anni (t = 10). Sostituendo questi valori nella formula, otteniamo:
A = 1,000(1 + 0.18/1)^(1*10)
= 1,000(1 + 0.18)^10
= 1,000(1.18)^10
≈ 5,054.08 euro
Quindi, dopo 10 anni, con una crescita del 18% all’anno e l’interesse composto, avrai circa 5,054.08 euro a tua disposizione.
6. Se compro 10.000 euro in azioni e le tengo per 10 anni, considerando una crescita del 15% ogni anno, considerando una tassazione annuale sugli interessi del 26% , dopo 10 anni quanti soldi avrò in totale? ( considerando l’interesse composto)?
Per calcolare la somma totale che avrai a disposizione dopo 10 anni con una crescita del 15% all’anno, considerando una tassazione annuale del 26% sugli interessi e l’interesse composto, dobbiamo tenere conto dell’imposta sul reddito generata dagli interessi accumulati.
La formula per calcolare l’importo finale con l’interesse composto e l’imposta sul reddito sugli interessi è simile a quella dell’interesse composto, ma bisogna considerare l’imposta come una riduzione dell’importo accumulato:
A = P(1 + r/n)^(nt) * (1 – t)
Dove:
A = L’ammontare finale comprensivo degli interessi
P = L’importo principale iniziale
r = Tasso di interesse annuale (in decimale)
n = Numero di volte in cui l’interesse viene composto all’anno
t = Tasso di imposta sul reddito generato dagli interessi (in decimale)
Nel tuo caso, hai 10.000 euro (P), un tasso di crescita del 15% (r = 0.15) e una tassazione annuale del 26% sugli interessi (t = 0.26). Supponiamo che l’interesse venga composto una volta all’anno (n = 1) per 10 anni (t = 10). Sostituendo questi valori nella formula, otteniamo:
A = 10,000(1 + 0.15/1)^(1*10) * (1 – 0.26)
= 10,000(1 + 0.15)^10 * (1 – 0.26)
= 10,000(1.15)^10 * 0.74
≈ 21,946.91 euro
Quindi, dopo 10 anni, con una crescita del 15% all’anno, considerando una tassazione annuale del 26% sugli interessi e l’interesse composto, avrai circa 21,946.91 euro in totale.
Altri termini finanziari da conoscere se vuoi investire soldi con il trading online
- Finanza comportamentale
- Stop Loss: come proteggere i Nostri investimenti
- Il migliore Trader italiano
- Quando comprare le azioni
- Quando vendere le azioni
- Orari di apertura delle Borse Valori
- Calendario Borse Valori 2021
- Rimbalzo del Gatto Morto
- Sell-Off
- Mercato Ribassista – Orso
- Credit Default Swap ( CDS )
- Cos’è il Campionato Mondiale di Trading
- Tasse su bitcoin e criptovalute
- EPS Utile per Azione
- Tazza e manico – Cup and Handle
- Come non pagare commissioni
- Trading Quantitativo
- High Frequency Trading
- EBITA
- Il rally di Babbo Natale
- Supporti e le resistenze
- Indice VIX
- Short Selling
- Leva Finanziaria
